What is Pascal’s Law? Applications of the law in industry

Pascal’s Law is an important physical principle that explains how pressure in a fluid is transmitted within a closed system. It is the foundation for the operation of modern hydraulic devices such as lifts or hydraulic jacks. In Vietnam, Naltako, a pioneer in providing hydraulic lifting equipment, has applied this principle to create high-quality products such as scissor lifts, hydraulic lift tables, and dock levelers. This article will clarify what Pascal’s Law is, its formula, applications, and how Naltako leverages it to provide optimal solutions for the industry.

What is Pascal’s Law in physics?

Pascal’s Law, also known as Pascal’s principle, states that: The pressure increase in an incompressible fluid (such as hydraulic oil) in a closed container is transmitted undiminished to every point in the fluid and the walls of the container. In other words, when you apply a small force at one point, the pressure spreads evenly throughout the system, creating a force amplification effect. This principle is the core of hydraulic systems, helping to convert a small force into a large force to lift heavy objects.

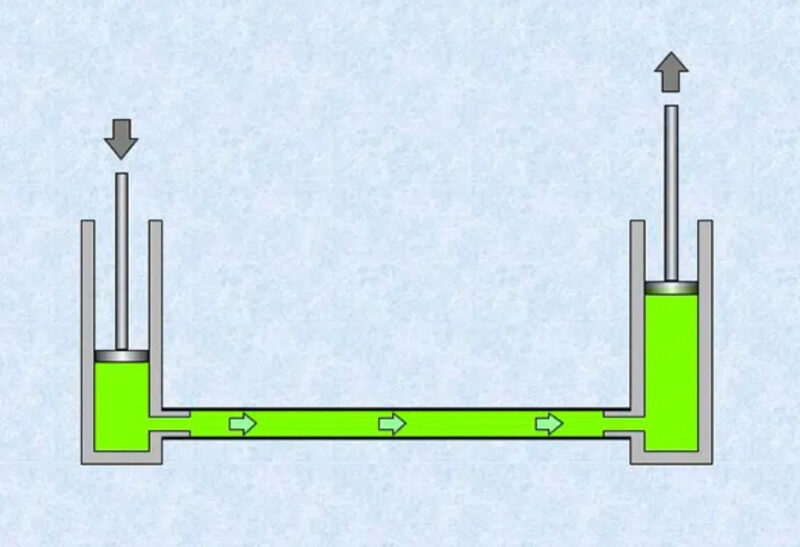
In practice, this law is vital for industries using hydraulic equipment. At Naltako, Pascal’s principle is applied in the design of products like hydraulic lift tables and hydraulic pallet trucks. For example, when a user pumps oil into the cylinder of a hydraulic pallet truck, the pressure is transmitted evenly throughout the system, creating a powerful lifting force to move heavy pallets of goods. Similarly, hydraulic lift tables utilize fluid pressure to lift and lower goods easily, saving labor effort.

Gravitational acceleration (g ≈ 9.807 m/s²) also plays a role in pressure calculation, ensuring the equipment operates stably. Naltako’s products are not only durable but also safe, meeting the rigorous demands of heavy industries such as logistics, construction, and manufacturing.

Applications of pallet cages today

What is the formula for Pascal’s Law?

The fluid pressure formula according to Pascal’s Law is expressed as follows:

[ p = p_a + \rho g h ]

Where:

• ( p ): Pressure at the considered point in the fluid.
• ( p_a ): External pressure (usually atmospheric pressure).
• ( \rho ): Density of the fluid (e.g., hydraulic oil).
• ( g ): Gravitational acceleration, approximately 9.807 m/s².
• ( h ): Height of the fluid column from the considered point to the surface.

This formula shows that fluid pressure increases with depth and is influenced by external pressure. In a closed hydraulic system, pressure is transmitted evenly without reduction, generating a large lifting force from a small initial input force. This is the exact principle that Naltako applies to optimize equipment like freight elevators.

For instance, in freight elevators, Naltako engineers calculate the piston area and oil pressure to ensure the lifting force is strong enough to lift large loads efficiently. With gravitational acceleration (g ≈ 9.807 m/s²) being a constant, adjusting factors like ( \rho ) and ( h ) helps the equipment operate accurately and safely. This technology is also applied in hydraulic lift tables, bringing superior performance to users.

What is a safety valve? Common types of safety valves today

Applications of Pascal’s Law in daily life?

Pascal’s Law is present in many aspects of life and industry thanks to its ability to transmit fluid pressure effectively:

• Hydraulic lifts: Such as Naltako’s dock levelers, supporting the movement of goods at seaports.
• Hydraulic jacks: Used to lift cars or heavy objects in construction with little force.
• Hydraulic braking systems: Transmitting pressure from the pedal to the wheels, ensuring traffic safety.
• Hydraulic presses: Applied in industry to compress metal or plastic.

At Naltako, this principle is integrated into products like mini cranes and scissor lifts. For example, dock levelers use hydraulic systems to adjust the height, helping to load and unload goods from trucks to containers without much effort. These devices are not only efficient but also ensure safety, suitable for heavy industries.

Structure of a motor and its operating principle

Illustrative example of Pascal’s Law?

Imagine a simple hydraulic jack system:

• You apply a small force ( F_1 ) to a small piston (area ( A_1 )), creating pressure ( p = \frac{F_1}{A_1} ).
• According to Pascal’s Law, this pressure is transmitted undiminished to a larger piston (area ( A_2 )), generating a lifting force ( F_2 = p \times A_2 ).
• Since ( A_2 ) is larger than ( A_1 ), the force ( F_2 ) will be many times larger than ( F_1 ).

For example, if the piston area ratio is 1:10, the lifting force will be 10 times the original force. This is how Naltako designs products like scissor lifts. In these devices, fluid pressure transmitted through hydraulic cylinders helps lift large loads safely and effectively, even with only a small input force from the operator.

Who discovered Pascal’s Law?

Blaise Pascal, a French scientist, laid the foundation for Pascal’s Law in the 17th century. Through experiments with closed containers containing liquid, he discovered that pressure is transmitted unchanged throughout the system. The law was officially published in 1663, becoming the foundation for modern hydraulic engineering.

Pascal’s invention changed how humans apply fluid pressure in industry. At Naltako, this principle is used in equipment like tilting lift tables, helping to handle bulk materials efficiently thanks to the strong lifting force from the hydraulic system. The combination of science and technology has helped Naltako affirm its position in the field of lifting equipment in Vietnam.

Partner with Naltako to own high-quality hydraulic equipment! Contact us at 0981.977.898 today!